DOS
El problema se plantea así:
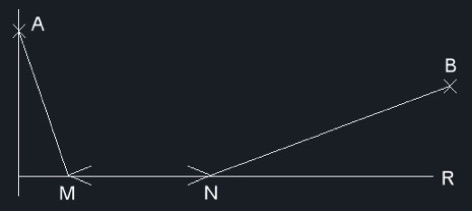
Dados los puntos A y B y la recta R, situar sobre ésta el segmento MN de longitud conocida, de forma que AM / BN = a / b siendo a y b dos números enteros cualesquiera. La Fig. 8 coloca el segmento MN en una posición arbitraria.
Fig. 8
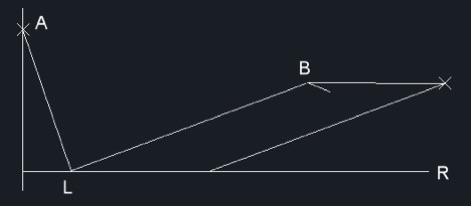
Fig. 9
Buscaremos la solución al trasladar BN de Fig. 8 haciendo coincidir M y N. Llamaremos L al punto de coincidencia (Fig. 9).
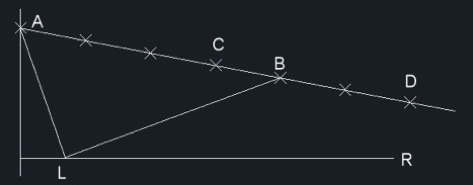
Si hacemos, por ejemplo, a = 3 y b = 1 habríamos de tener que AL / BL = 3 / 1 = 3. Tal cosa no ocurre en la Fig. 9, así que seguiremos indagando en la Fig. 10
Fig. 10
En esta Fig. 10 vemos que los puntos C y D cumplen las condiciones exigidas: AC / BC = 3 / 1 y AD / BD = 3 / 1. Como se ve, C es interior del segmento AB y D es exterior.
Además, la circunferencia de diámetro CD es el lugar geométrico de los puntos que cumplen la condición exigida. Demos por supuesto que esto es así (Olabarrieta, teorema 63). La Fig. 11 muestra esa circunferencia produciendo el punto L en su intersección con R. Supondremos, pues, que L es el punto buscado.
Pero existe además otro teorema de fácil demostración (Olabarrieta, teorema 62) que expresa:
En todo triángulo (el LAB por ejemplo), la bisectriz de un ángulo (la LC del ALB) y la del ángulo externo correspondiente (la LD del BLH) dividen al lado opuesto (el AB) en dos segmentos proporcionales a los lados del ángulo (CA / CB = LA / LB y DA / DB = LA / LB).
Dado el cumplimiento de este teorema y el hecho de que ALH es un ángulo llano, las bisectrices LC y LD han de formar un ángulo recto. Cosa que es cierta al estar L en la circunferencia de diámetro CD.
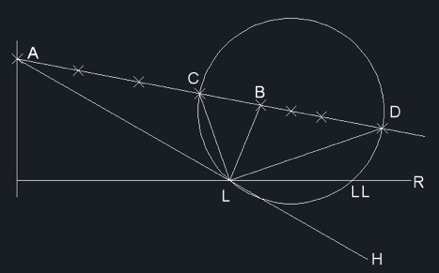
Por las mismas razones expuestas LL será otro punto que cumple la condición LL A / LL B = 3. Tenemos pues, dos soluciones al problema. Habría sólo una si la circunferencia fuera tangente a R o no habría solución si las condiciones condujeran a que la circunferencia no llegara a cortar a R.
En la Fig. 12 se ve la solución LL después de deshacer la traslación MN que se produjo en la Fig. 9.
Fig. 11
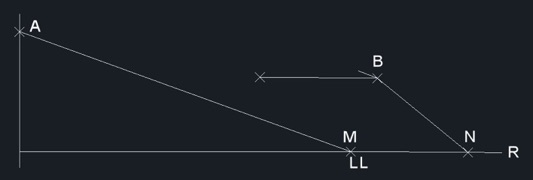
Fig. 12
oooo0oooo
Este último problema pontificio muestra otra complicación. Se trata de unir los pueblos A y B que separan dos ríos; hay que construir el camino más corto entre dichos pueblos que incluya sendos puentes perpendiculares a las respectivas orillas de los ríos.
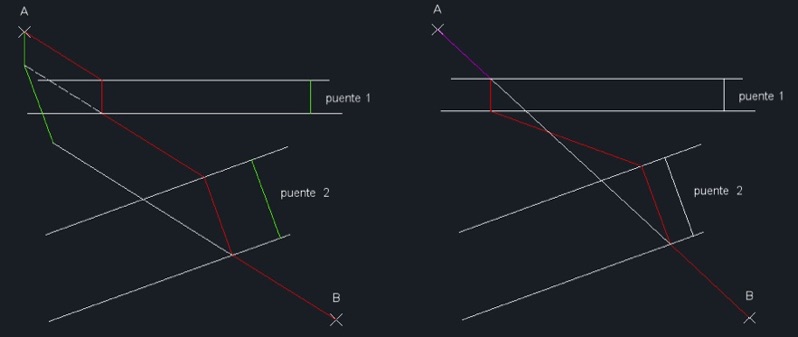
Enter Text
La figura de la izquierda es la cientofica; la de la derecha es la intuitiva; ésta resulta ser 1,59 % más larga que la otra (según se puede medir en Autocad para este caso). En ambas se muestra en rojo el camino resultante.
Lo primero que se hace en la figura de la derecha es trazar AB; el resto resulta evidente.
La solución de la izquierda es muy elegante. Desde A hacia abajo se construye la quebrada verde cuyo extremo inferior se une con B. A partir de ahí queda claro cómo han de hacerse las demás uniones. El paralelismo de las bases de los dos romboides justifica que la quebrada roja sea la de longitud mínima.
PAG. 3 / 3