Estos dos problemas que siguen no son realmente muy fluviales: son más bien aeronáuticos, porque verán lo que pasa.

Parece ser que la ley exige que las carreteras interestatales en Estados Unidos tengan una milla recta de cada cinco, para uso como pista de aterrizaje en casos de emergencia y de guerra.

DOS 1

El problema se plantea así:

Dados los puntos A y B y la recta R, situar sobre ésta el segmento MN de longitud conocida, de forma que AM + MN + NB sea mínimo. La Fig. 5 coloca el segmente MN en una posición arbitraria.

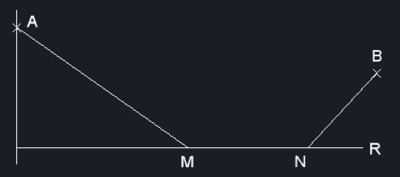
Fig. 5

En la Fig. 6 se ven las operaciones necesarias para conseguir la solución: Se traslada B paralelamente a R una distancia igual a MN, obteniendo B´; B´´, simétrico de B´ respecto de R se une con A para obtener M. A partir de M se lleva el segmento MN sobre R y se une N con B. Así se obtiene el trayecto buscado AMNB.

Ese trayecto sería mínimo si lo fuera AMB´. Tal ocurre al ser AB´´ una recta y MB´´ = MB´ = NB.

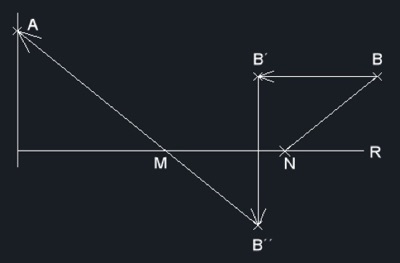
Fig. 6

Obtenida esta elegante solución puramente geométrica vamos a ver otra en geometría analítica con recursos algebraicos y de cálculo diferencial.

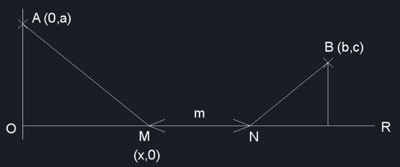
Fig. 7

La Fig. 7 es como la 5 pero mostrando R como eje de las x, O como origen, y las coordenadas de los diferentes puntos. Asimismo haremos d = b – m.

Llamando y a la función que representa al recorrido AMNB, será:

Enter Text

Derivando:

Igualando y´ a cero obtendremos el valor de x que produce y mínima.

Hay que observar que habiendo situado AMNB dentro de las perpendiculares por A y por B, siempre obtendremos la y mínima. La máxima será para un valor infinito cuando MN se saque de ese espacio. Para y´ = 0 se tiene:

Para que la suma de estas dos fracciones valga cero basta que sea cero el numerador del quebrado suma, con tal de que el denominador de dicho quebrado suma no sea infinito ni imaginario. Ambas condiciones se cumplen en nuestro caso una vez situados entre las verticales por A y B.

Operando se tiene esta ecuación de segundo grado de coeficientes conocidos:

De ella se obtienen dos valores para x: uno es válido y el otro descartable por resultar mayor que b. Midiendo sobre la Fig. 7 y resolviendo la ecuación se puede comprobar que el resultado es satisfactorio.