Pgs. 1 2
GEOMETRÍA DE MASAS
Vuelto mi amigo de Valladolid me suministró abundante información sobre el tema de forma que pude revisar lo que ya tenía escrito y acometer cosas nuevas. Como bibliografía quiero recomendar, aparte de la obra de Javier Gª Capitán, a Hausner (The Center of Mass and Affine Geometry) y a Rike (Mass Point Geometry).
En estas condiciones podemos ver otra orientación del PROBLEMA 1 asociado a la Fig. 3. En la Fig. 30 se muestra el mismo RST de Fig. 3 pero aplicando la notación de la Geometría de Masas que usa la más cómoda representación en 2D frente a la de 3D que yo había utilizado. Asimismo supone una gran simplificación el sencillo empleo que hace de la ley de la palanca: Potencia por su brazo, igual a resistencia por el suyo.
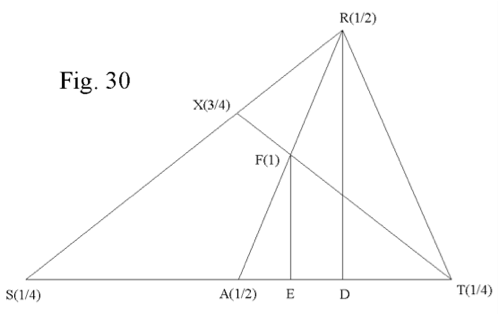
Si en Fig. 3 suponemos que VF = 1, también será VR = 1/ 2 y VS = VT = 1 / 4
En la Fig. 30 se aprecia la diferencia de las dos notaciones: VR = 1/ 2 queda como R (1/2), etc.
Se ve asimismo que X( ) = R(1/2) + S(1/4) = 3/4 que nos permite escribir X(3/4).
Análogamente será:
A( ) = S(1/4) + T(1/4) = 1/2 que nos conduce a A(1/2).
Comprobándose que
F(1) = R(1/2) + A(1/2)
Así como que F(1) = R(1/2) + S(1/4) + T(1/4)
Por fin podremos escribir:
S(1/4) * XS = R(1/2) * RX RX / XS = (1/4) / (1/2) = 1/2
Nueva orientación del PROBLEMA 2
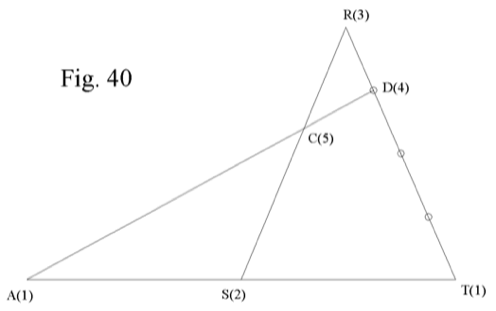
La Fig. 40 es equivalente a la Fig. 4.
Lo que inicialmente sabemos de ella es la situación de S y D, respectivamente, en AT y RT. Eso nos permite asignar pesos a los diferentes puntos. Así, si establecemos A(1) veremos que es T(1) con fulcro en S de forma que será S(2). Al haber resultado T(1) y, dado cómo está dividido RT, será R(3) y D(4).
C(5) es consecuencia de A(1) y D(4). Al mismo resultado habríamos llegado si hubiéramos empezando asignando pesos a R y T. En estas condiciones tendremos:
R(3) * RC = S(2) * CS RC / CS = 2/3
D(4) * DC = A(1) * CA DC / CA = 1/4
PROBLEMA 3
Sea el ABC de la Fig. 50, con sus lados divididos en partes iguales según se muestra.
Hallar XO / OY, y BO / OZ.
Observamos en primer lugar que no todas las rectas interiores al triángulo son cevianas (las que parten de los vértices hacia sus lados opuestos): XY es una transversal. En casos así, la geometría de masas exige una condición: Para hacer la asignación de masas hay que empezar por el vértice ceviano girando alrededor del triángulo para volver al mismo vértice de inicio (el B en este caso). Así nos encontraremos en B con dos valores de masa, el inicial y el final. Pues bien, la masa en B será la suma de ambas. Es lo que en inglés se llama mass splitting (fragmentación).
En la figura de la derecha se han asignado valores de masa a los respectivos puntos en función de la disposición de cada segmento pensado como balancín con su fulcro correspondiente.
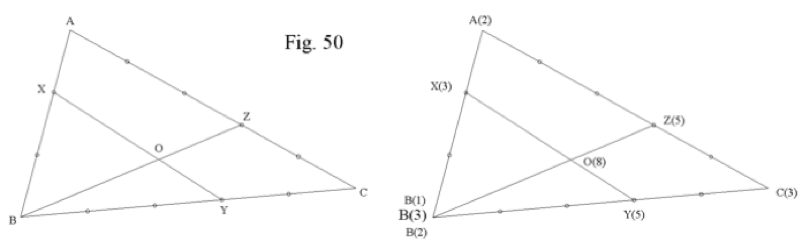
Así pues será:
B(3) * BO = Z(5) * OZ BO / OZ = 5 / 3
X(3) * XO = Y(5) * OY XO / OY = 5 / 3
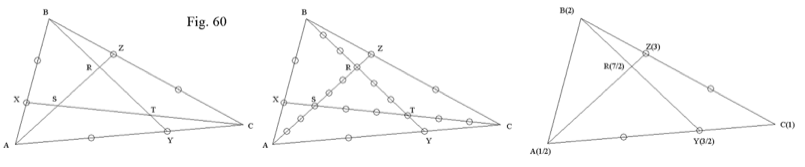
UNA CURIOSIDAD (Fig. 60)
Probar que si en un ABC se dividen sus lados según la imagen de la izquierda, sus cevianas quedan segmentadas como se ve en la figura del centro.
En la figura de la derecha se muestran sólo las cebianas correspondientes a los vértices A y B. Empezando por éste, y en sentido horario, se hace la adscripción de masas tal como se muestra.
R será el centro de masas de manera que B(2) + Y(3 / 2) = R(7/2) al igual que A(1 / 2) + Z(3) = R(7/2).
Asimismo será:
B(2) * BR = Y(3 / 2) * RY BR / RY = (3 / 2) / 2 = 3 / 4
A(1 / 2) * AR = Z(3) * RZ AR / RZ = 3 / (1 / 2) = 6 que es cosa comprobable en la figura central. Haciendo lo mismo con los otros dos pares de cevianas, se completa la prueba.
PROBLEMA 4
En el triángulo ABC (Fig. 70), tomemos E sobre AC tal que AE:EC=1:2, tomemos F sobre BC tal que BF:FC=2:1, y tomemos G sobre EF tal que EG:GF=1:2. Finalmente tracemos el recta CG que intersecará a AB en el punto D. Encontrar CG:GD y AD:DB
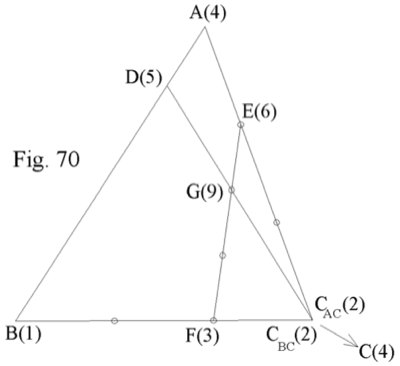
Hay que observar que las masas han sido asignadas a los puntos después de seguir el proceso que se muestra a continuación.
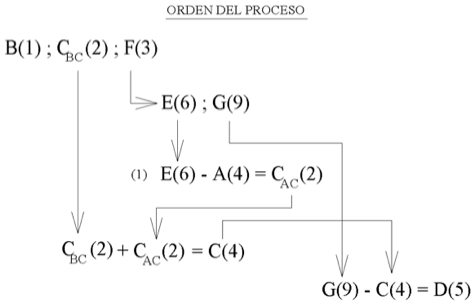
Con la nota (1) se quiere indicar que esa igualdad equivale a haber resuelto el siguiente sistema de ecuaciones que da como resultado A(4) y CAC(2).
A + CAC = 6
A * 1 = CAC * 2
PAG. 2 / 2