Pgs. 1 2
Con toda la información precedente, vamos a calcular la longitud de una de las curvas (la que describe B); todas son iguales: coinciden si se giran 90 º en sentido antihorario.
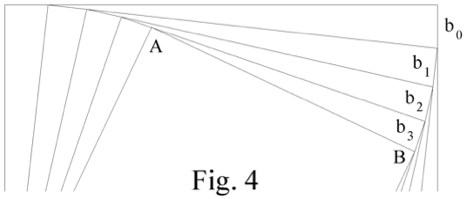
La Fig. 4 es una ampliación parcial de la 3. En ella llamaremos b0 a la primera carrerita de B ( BB1 de Fig. 1); sucesivamente se tienen los siguientes tramos de la curva b1 b2 b3 … Llamando d0 al lado del cuadrado inicial (los 10 m de lado del patio -AB de Fig. 1-), tendremos:
b0 = 0,1 d0 = 0,1 d0
b1 = 0,1 d1 = 0,1 x 0,90553851 d0
b2 = 0,1 d2 = 0,1 x 0,905538512 d0
b3 = 0,1 d3 = 0,1 x 0,905538513 d0
……………
bn = 0,1 dn = 0,1 x 0,90553851n d0
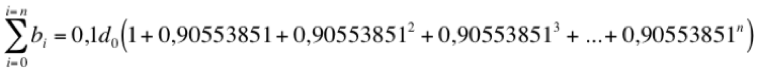
Los sumandos que siguen a la unidad dentro del paréntesis constituyen la suma de los términos de una progresión geométrica de razón menor que uno cuyo valor es a1 / (1-r), siendo a1 el primer término de la progresión y r su razón. En nuestro caso ambos son iguales y valen 0,90553851. Así pues, tendremos:
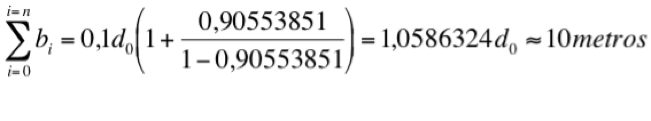
Se confirma la paradoja que se da en una progresión geométrica de este tipo: tiene un valor fijo, pero inalcanzable.
Ya se ve que la aproximación no es demasiado buena. Lo cibernético es mucho mejor. Sin embargo, si los muchachos hubieran dado su carrerita inicial de 1 cm en vez de darla de 1 metro, el resultado final sería de 10,005003 metros en vez de los 10,586324.
Enter Text
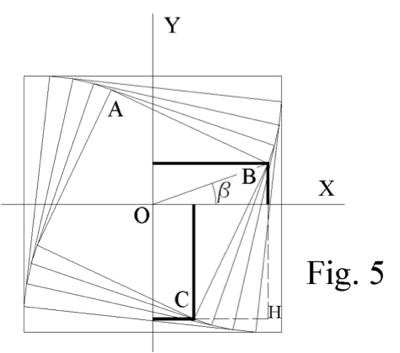
En la Fig. 5 ya se apunta la tendencia de la trayectoria de B que resulta plenamente confirmada en la 2 como de una espiral. Veámoslo en la Fig. 5 donde aparecen en grueso las coordenadas del perseguidor B y del perseguido C. La tangente a la curva de B en B es BC la hipotenusa del triángulo rectángulo BCH; la tang. del ángulo BCH (igual a dy / dx), representa la derivada de la curva en el punto B.
La pendiente de la recta tangente BC a la curva en B, tomando valores absolutos, es
dy / dx = tang BCH = BH / HC = (YB + YC) / (XB - XC)
Poniendo esta última fracción en función de las coordenadas de B, será
dy / dx = (YB + XB) / (XB – YB)
Generalizando el punto B a cualquiera de la función-trayectoria de B, tendremos:
dy / dx = (x + y) / (x-y) ( 1 )
El punto B, en coordenadas polares vendrá representado por su radio vector r = OB, su ángulo β y las siguientes relaciones (recordar que tanto r como β son variables):
x = r cos β y = r sen β
dx = cos β dr – r sen β d β
dy = sen β dr + r cos β d β
Llevando estos cuatro últimos valores a (1), se tiene:
(sen β dr + r cos β dβ) / (cos β dr – r sen β dβ) = (r cos β + r sen β) / (r cos β - r sen β)
que simplificando queda reducida a
dr = r dβ (2)
que es la ecuación diferencial de la curva seguida por los niños. La ecuación de una espiral logarítmica es (Puig Adam, Cálculo Integral):
en la que podemos hacer a = 1 al ser a el factor de escala que determina el tamaño de la espiral, resultando
Derivando:
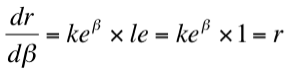
que al comparar con (2) muestra que la curva de persecución que hemos tratado es una espiral logarítmica.
Obtenida (2), se puede integrar la ecuación diferencial, en coordenadas polares, para calcular la longitud de la curva.
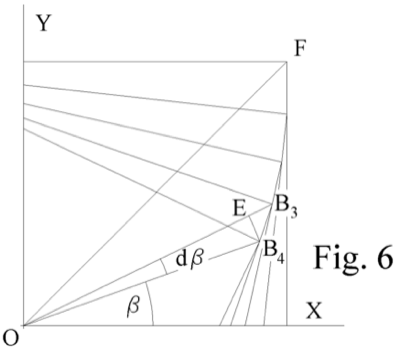
La Fig. 6 es una extracción, aumentada, de la 5. En ella OB4 = OE es el radio vector r y EB3 es dr. El triángulo EB3B4, en el límite, será un triángulo rectángulo isósceles en el que tendremos:
EB4 = OB4 x dβ = r x d β = dr
EB3 = dr
B3B4 = ds (hipotenusa: diferencial de la longitud de curva S)
La curva habrá de ser integrada en el cuadrante representado, entre los valores de r comprendidos entre O y F, es decir, entre r = 0 y r = OF = (l0 / 2) x √ 2 = l0 / √ 2.
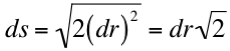
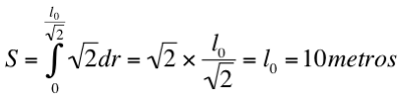
La integración produce la exactitud que se echaba de menos acudiendo a una progresión geométrica.